工具变量(Instrumental-Variable)本身是一个计量经济学的概念,它的出现是为了克服普通最小二乘法中的内生性问题。
内生性问题
内生性问题的原因主要有以下三种
- 遗漏变量
- 变量有测量误差
- 双向因果关系:比如受教育年限影响工资,工资反过来影响受教育年限
假设
孟德尔随机化需要三个核心工具变量假设,即:
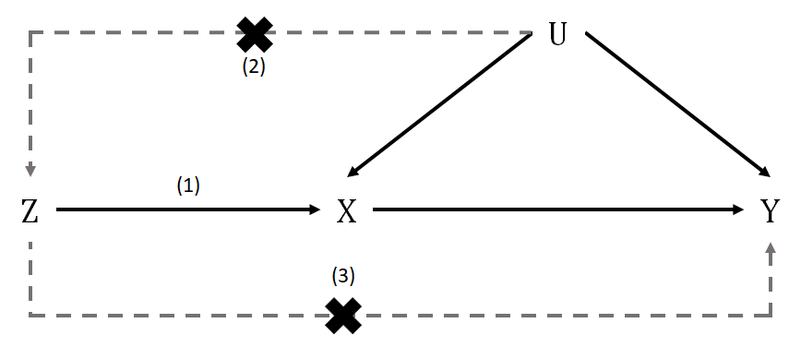
- 相关性假设:用作工具变量的遗传变异 (\(Z\) )与暴露 (\(X\)) 有关,即存在 \(Z \to X\)
- 独立性/可交换性假设:遗传变异和目标结果没有共同的原因(即没有干扰因子),即虽然可能存在 \(U \to Y\),但是不存在 \(U \to Z\)
- 排斥性/无水平多效性假设:除了通过暴露( \(X\) )外,遗传变异( \(Z\) )和结果( \(Y\) )之间没有独立的因果途径,不存在 \(Z \to Y\) 不经过 \(X\)
模型解释
- 用作工具变量的遗传变异( \(Z\) )
- 暴露( \(X\) )
- 结果( \(Y\) )
- 混杂因素( \(U\) )
模型使用
使用两阶最小二乘(Two Stage Least Squares,TSLS)来替代原来的最小二乘法
\[Y = \sum \beta_i X_i + \delta\]
第一步:建立自变量\(X\)和工具变量的回归模型
\[X = \alpha Z + \epsilon\]
在这一步中,需要验证,\(Cov(Z, \epsilon)=0\),也即工具变量和混杂因素无关。 注:我感觉应该是残差吧!
另外还需要考虑上述方程的决定系数或者说是F统计量,来判断\(Z\)和\(X\)的关联强度。通常情况下,决定系数或者F统计量越大,说明Z和X的关联程度越大。
第二步:将第一步中拟合的X的估计量带入如下方程:
\[Y = \beta \hat{X} + \delta\]
其中\(\beta\)便是\(X\)对\(Y\)的纯净效应量。